Magnitude
Magnitude refers to the brightness of a star or object. The first person to assign magnitude numbers to stars was the ancient astronomer Hipparchus, who categorized stars into six levels of brightness, 1 being the brightest and 6 being the faintest. The system we use today is similar to that created by Hipparchus, though more modern methods are used to come up with the numbers.
The modern magnitude scale was developed in the 1850's and works in a similar was to Hipparchus' scale, with brighter stars receiving smaller numbers. In the modern scale, a 1st magnitude star provides 100 times the illumination that a 6th magnitude star does. This means that the 5th root of 100 is the brightness difference between any two successive magnitudes. So a 1st magnitude star is 2.512 times as bright as a 2nd magnitude star. The formula defining the ratio of magnitudes between two different stars is:
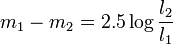
Where 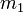 is the magnitude of the first star,
is the magnitude of the first star, 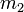 the magnitude of the second star,
the magnitude of the second star, 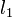 the light flux of the first star and
the light flux of the first star and 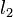 the light flux of the second star.[1]
the light flux of the second star.[1]
Magnitude is an important measure of an object as it can allow us to gage if it is visible or not. Limiting magnitude is the dimmest object that can be seen with a particular optical system. See the article on limiting magnitudes for more information on this.
Contents |
Types of Magnitude
There are many types of magnitude, all using the same scale. Each measures a slightly different thing such as a particular kind of light, or put a start at a certain distance. For most cases in amateur astronomy, there are three types to be aware of: apparent visual, absolute visual and bolometric magnitudes.
Apparent Visual Magnitude
Apparent visual magnitude, sometimes just called visual magnitude or apparent magnitude, is how bright the star or object appears to us here on Earth. It is a measure of the light that we receive at the telescope in the visual band, in other words the spectrum as our eyes see it. This is the magnitude scale most often used by amateur astronomers as it tells them if an object will be visible or not given the limiting magnitude of their optical systems.
Absolute Visual Magnitude
Light obeys an inverse square law. This means the farther you are from an object, the dimmer it will appear. Thus since stars can vary in brightness due to either their distance or their actual or intrinsic brightness, there needs to be a way to compare how bright stars actually are. This is where absolute magnitude comes in. Absolute magnitude is defined by astronomers as how bright a star would look at a standard distance. The distance that has been chosen by astronomers is 10pc. This gives a way of comparing the brightness of stars as now only the stars' intrinsic brightness is a factor. As with apparent visual magnitude, absolute visual magnitude refers to the absolute brightness in the visual band.
To compute absolute magnitude you need to know two things, the apparent magnitude and the distance. Conversely if you know the absolute and apparent magnitudes you can work out the distance (ignoring for now the interstellar extinction caused by dark nebulae). The formula for working this out is:
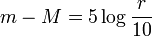
Where m is the apparent magnitude of the star, M is the absolute magnitude of the star and r is the distance to the star in parsecs.[1]
Bolometric Magnitude
You may occasionally hear reference to an object's bolometric magnitude. The bolometric magnitude of a star or other object is the total amount of energy from all parts of the electro-magnetic spectrum received from that object. This contrasts to the visual magnitude which looks at only the tiny amount of energy that our eyes can see. This means that a star's bolometric magnitude is more directly related to the star's total luminosity, or the amount of energy it puts out every second. As with visual magnitude, bolometric magnitude can be apparent or absolute.
Magnitude of Extended Objects
So far we have looked at the magnitude of stars. The apparent magnitude of a star is fairly representative of how bright the star is as the star is a point source, that is all the energy appears to be coming from a single point in space. Extended objects such as galaxies, nebulae and clusters aren't point sources. This means that their magnitudes are a little more deceptive as the energy that we are seeing is spread out over a portion of the sky in a way that stars aren't. Thus the apparent magnitude reported for extended objects are actually a representation of the total energy received from all parts of the object.
This means that if we have two extended objects and a star of the same magnitude, they may all appear to have different brightness when looked at by the eye. The star will appear as the stated magnitude, since it is a point source. The other two objects will appear dimmer than the star, despite having the same apparent magnitude, because the energy is spread out over a larger area. One object may even be harder to see than the other because it's surface brightness might be lower. Surface brightness is the magnitude per unit area of object. So two objects with the same reported magnitude but different areas may not appear equally bright as the larger object must put out the same energy over a larger area. This makes a the larger object appear dimmer than the smaller object. It would also make the larger object harder or impossible to see.