Mass determination
| Line 7: | Line 7: | ||
and p is the period of the planet in years and a is the semi-major axis of the planet in astronomical units. | and p is the period of the planet in years and a is the semi-major axis of the planet in astronomical units. | ||
| − | + | ==Mass determination with one object much more massive than the other== | |
If the object is orbited by a much smaller object, such as a planet about a star, moon or spacecraft about the planet then we can use Newton's form of Kepler's third law. | If the object is orbited by a much smaller object, such as a planet about a star, moon or spacecraft about the planet then we can use Newton's form of Kepler's third law. | ||
| Line 25: | Line 25: | ||
So an example: Jupiter's moon Io takes 1.769 days to make one orbit. It's semi-major axis is measured to be 421800km. From this we can work out Jupiter's mass. Converting days to seconds gives us a period of <math>1.528\times10^{5}</math>s and a semi-major axis of <math>4.218\times10^{8}</math>m. Substituting in to our equation above gives us a mass of about <math>1.9\times10^{27}</math>kg or about 318 times the mass of the Earth. | So an example: Jupiter's moon Io takes 1.769 days to make one orbit. It's semi-major axis is measured to be 421800km. From this we can work out Jupiter's mass. Converting days to seconds gives us a period of <math>1.528\times10^{5}</math>s and a semi-major axis of <math>4.218\times10^{8}</math>m. Substituting in to our equation above gives us a mass of about <math>1.9\times10^{27}</math>kg or about 318 times the mass of the Earth. | ||
| − | + | ==Mass determination with both objects are close in mass== | |
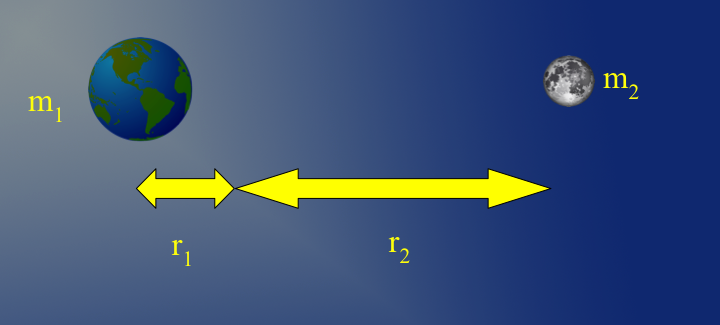
For objects that are close in mass we need to do something else since the two objects will orbit about a common [[barycentre]]. As it turns out the distance from the centres of the bodies is related to the mass of the two bodies thus: | For objects that are close in mass we need to do something else since the two objects will orbit about a common [[barycentre]]. As it turns out the distance from the centres of the bodies is related to the mass of the two bodies thus: | ||
Latest revision as of 08:33, 2 August 2015
Determining the mass of an object in space is can be done one of two ways. One way if the object is being orbited by another body that is much less massive than the primary, such as a planet orbiting a star. The other way is used when two objects with relatively close masses are orbiting each other. Using these two variations on a theme, we have been able to measure the mass of our Sun, the other planets in our solar system, other stars and even whole galaxies.
Both cases use a form of Kepler's third law of planetary motion, where:
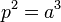
and p is the period of the planet in years and a is the semi-major axis of the planet in astronomical units.
[edit] Mass determination with one object much more massive than the other
If the object is orbited by a much smaller object, such as a planet about a star, moon or spacecraft about the planet then we can use Newton's form of Kepler's third law.
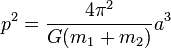
With 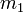 being the mass of one body and
being the mass of one body and 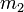 being the mass of the other. If one body,
being the mass of the other. If one body, 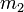 is much less massive than the other, it can be safely ignored, dropping it out of the equation thus:
is much less massive than the other, it can be safely ignored, dropping it out of the equation thus:
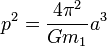
At this point we can solve for 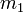 giving us:
giving us:
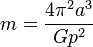
Since G is usually given in MKS units as 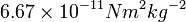 the semi-major axis (a) and period (p) also need to be in MKS units, metres and seconds respectively.
the semi-major axis (a) and period (p) also need to be in MKS units, metres and seconds respectively.
So an example: Jupiter's moon Io takes 1.769 days to make one orbit. It's semi-major axis is measured to be 421800km. From this we can work out Jupiter's mass. Converting days to seconds gives us a period of 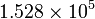 s and a semi-major axis of
s and a semi-major axis of 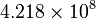 m. Substituting in to our equation above gives us a mass of about
m. Substituting in to our equation above gives us a mass of about 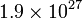 kg or about 318 times the mass of the Earth.
kg or about 318 times the mass of the Earth.
[edit] Mass determination with both objects are close in mass
For objects that are close in mass we need to do something else since the two objects will orbit about a common barycentre. As it turns out the distance from the centres of the bodies is related to the mass of the two bodies thus:
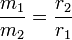
So we can, from the ratio and Kepler's Third Law work out the mass of stars that orbit each other based on these two relations:
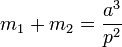
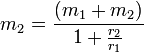
Where a is the separation distance in astronomical units and p is their orbital period in years. This yields masses in solar mass units (Sun's mass = 1).
So if we observe two stars orbiting each other with a separation of 100 AU and a period of 90 years and we work out that the barycenter is 25 AU from one of the stars we can do the following:
The total mass of the system from 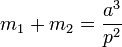 is:
is:
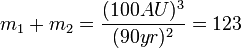 solar masses.
solar masses.
Using 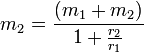 nets us the mass of one of the stars:
nets us the mass of one of the stars:
 solar masses.
solar masses.
Since we know the total mass of the system we can do some subtraction and find the other star's mass of 92.25 solar masses.